1. 具体数学第一节
2. 汉诺塔问题
经典河内塔问题中,有 3 根柱子和 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按从大到小依次套在一根柱子上,现在想将所有的圆盘按照原来的位置从一根柱子移动到另一根柱子上,移动过程需要遵守一些规则:
1.每次只能移动一个盘子
2.盘子只能从柱子顶端滑出移动到下一根柱子
3.盘子只能叠在没有盘子的柱子或者比它大的盘子上
河内塔的规则,限定了较大的圆盘要先转移到目标柱子(选择的任意一根柱子)上,这时直接转移是不可行的,一定要利用其他柱子。问题中只有 3 根柱子,所以,另外一个柱子一定是要将 N-1 个圆盘按照从大到小堆起,(这个柱子我们叫它cache peg,存放柱),这才使得最大圆盘可以直接从原来位置转移到目标位置。
假设解决 N 个圆盘的移动需要时间,记 Tn :

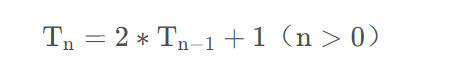

数学归纳法证明:


3. 直线分割平面问题:
一:N 条直线分割平面
假设,x 条线能将平面分为 f(x)份,这对于份 f(n) 第 n 条线,和其他 n-1 条线都有交点时,增加量最大,为 n;
则: f(n)=f(n-1)+n; f(n-1)=f(n-2)+n-1

有 f(0)=1;得到:n 条直线分割平面的数量最大为:f(n)=n*(n+1)/2 + 1;
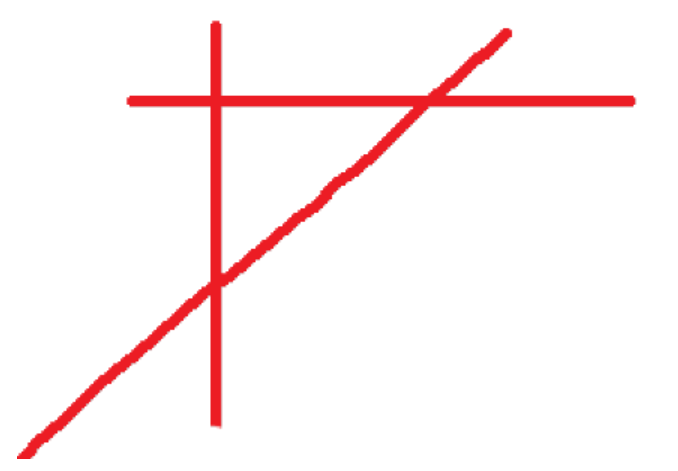
二. “V” 形线分割平面(折线)
对于“V”,我们可以把他们当成两条相交直线去掉两条射线。如下图:

上图为两条‘V’形线,对于每条‘V’形线,都相当于两条直线去掉后面两条射线,而去掉这两条射线会使平面减少 2,
因此,有直线公式转化得到: F(n)=f(2n)-2n=2n(2n+1)/2+1-2n;
三. ‘N’形线
N’形线分两种,一种是有两条平行边,二是没有平行边;
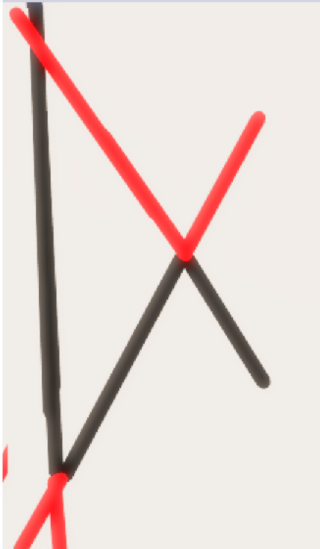
对于没有平行边的情况:
我们可以将其看成 3 条直线相交,然后去掉 4 条射线,去掉这 4 条射线后,会使平面相对于 3 条直线减少 6;
有直线公式可推得:
f(N)=f(3n)-6n=3n(3n+1)/2+1-6n;
如果是有平行:
情况则相对于没有的情况减少一个平面;
即为: f(N)=f(3n)=3n(3n+1)/2 + 1 - 5n;
4. 约瑟夫环问题
我们这个规则是这么定的:
在一间房间总共有 n 个人(下标 0~n-1),只能有最后一个人活命。
按照如下规则去排除人:
- 所有人围成一圈
- 顺时针报数,每次报到 q 的人将被排除掉
- 被排除掉的人将从房间内被移走
- 然后从被 kill 掉的下一个人重新报数,继续报 q,再清除,直到剩余一人
你要做的是:当你在这一群人之间时,你必须选择一个位置以使得你变成那剩余的最后一人,也就是活下来。
当 q = 2 时候,是一个特例,能快速求解
1.思路:注意这里的前提是 n = 2^k
如果只有 2 个人,显然剩余的为 1 号
如果有 4 个人,第一轮除掉 2,4,剩下 1,3,3 死,留下 1
如果是 8 个人,先除去 2,4,6,8,之后 3,7,剩下 1,5,除去 5,又剩下 1 了
我们仔细分析也就是每次除去一半的元素,然后剩余的一半继续重复之前的策略,再除去一半。(可想到递归)
结合:J(2) = 1 我知道两个数,从 1 开始,肯定是 2 先死,剩下 1.
定义 J(n)为 n 个人构成的约瑟夫环最后结果,则有j(2^k) = 1
2,假设 n = 2^k + t,t 可以随意取,比如 1,2,3…….
假设 n = 11,这时候 n = 2^3 + 3,也就是说 t = 3,所以开始剔除 3 个元素直到其成为 2^k 问题的约瑟夫问题。
So,我们在剔除了 t(3)个元素之后(分别是 2,4,6),此时我们定格在 2t+1(7)处,并且将 2t+1(7)作为新的一号,而且这时候的约瑟夫环只剩下 2^3,也就是 J(2^3 + 3) = 2*3 (剔除三个)+ 1(2^k 的约瑟夫问题) = 7,
答案为 7
总结一下这个规律:
J(2^k + t) = 2t+1
3,q 不等于 2 的情况下:
规律:Jq(n+1) = ( Jq(n) + q ) / (n+1)

其实就是从 q 开始,到之前最大数 n-1,每个数都减去 q,从 0 开始之后接着 n-1 这个新的值每次往后加 1,直到加到 n-1(这个下标)